 |
The figure shows the lepton-proton structure
function for diffractive events as a function of the virtuality Q2 of the
photon. The observable beta denotes the momentum of the scattered quark
measured relative to a colour neutral quark- gluon state which was emitted
by the proton. At small fractional energy xIP of this colour neutral state
relative to the proton beam energy this state is called pomeron. |
The measured
Q2 dependence of the structure function is consistent with flat. At the
large quark momentum shown, beta=0.4, the structure function looks different
from that of a hadron, for example that of the proton.
The dependence of a structure function on the virtuality Q2 of the
probing photon shows the contributions of quarks and gluons and is explained
by the QCD evolution equations:
d F2/d ln Q2 ~
Pqq fq + Pqg fg + Pqgamma
The terms Pij fj denote the convolution of a splitting function Pij
with a parton density fj. For example Pqg gives the probability of a
gluon splitting into a quark-antiquark pair, and fg denotes the gluon
density. The third term of the equation is relevant for the case of the
photon structure function only.
|
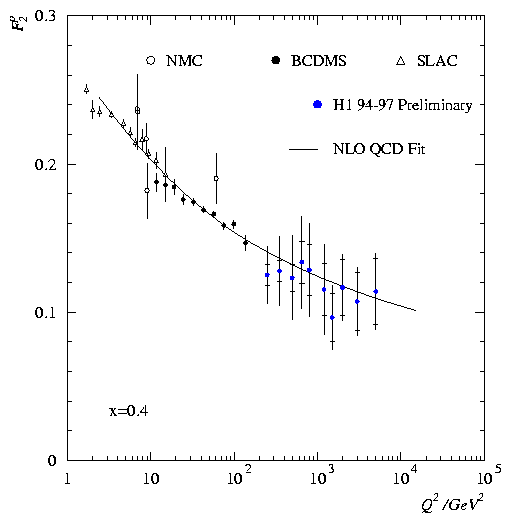 |
Comparison with Proton Structure:
The proton structure function at x=0.4 decreases as Q2 increases.
The probability to find a parton in the proton at large x decreases with
increasing resolving power Q2. |
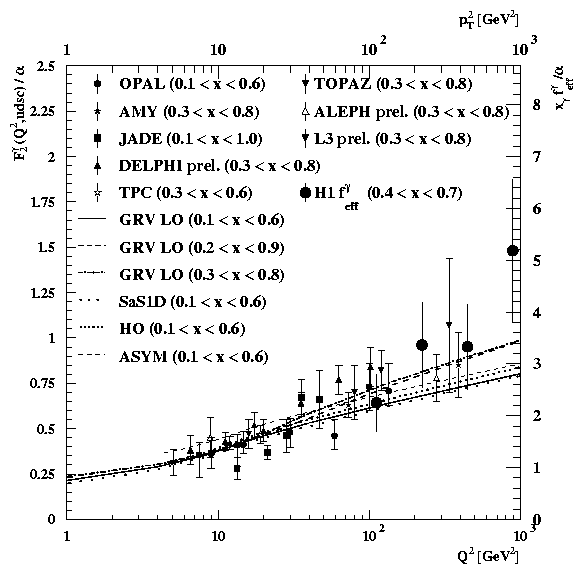 |
Comparison with Photon Structure:
The photon structure function at x=0.4
increases with Q2: the third term Pqgamma in the above equation denotes
the splitting of the photon into a quark-antiquark pair. This splitting
function is to first order independent of Q2 and generates the characteristic
logarithmic increase of the photon structure function with Q2. |
The flat shape of the structure function for diffractive
processes implies that the exchanged object cannot be a hadron consisting
of valence quarks.
The magnitude of the measured structure function excludes diffraction to
be caused by photon exchange. A consistent interpretation of the data
is given by a gluon dominated object. While in the case of the photon structure
function the splitting of a photon into a quark-antiquark pair is analysed,
the measurement of the structure function for diffractive exchange gives
information on the gluon splitting into a quark-antiquark pair and therefore
gives information on the structure of the gluon
(second term on the right hand side of the above equation).
The large gluon density of the exchanged object of diffractive processes
was confirmed in numerous measurements of the hadronic final state.
|




