Measurement of event shape variables in deep-inelastic scattering at HERA


The H1 Collaboration 


The electron proton collider HERA offers excellent possibilities to study strong interaction phenomena over a wide range of energy scales. In deep-inelastic scattering the basic reaction can be envisaged as scattering of an electron off a quark bound inside the proton. A particular clean reference system to separate the hard scattering process from the proton remnants is the Breit frame, where the struck quark collides head-on with the exchanged boson (i.e. a photon or Z-boson), and is backscattered into the current hemisphere. In this scheme, the direction of the boson provides a `natural' event axis and the momentum transfer $ Q$ carried by the boson is an obvious choice of energy scale. In the parton model picture the scattered quark has no transverse momentum and hadronises into a narrow, pencil like jet of particles. In reality, however, the final state quark is accompanied by multiple QCD gluon radiation leading to multi-jet configurations and the parton fragments are getting distributed more spherical.

The event topology or energy flow of the particles emitted in the current hemisphere is conveniently described by a variety of event shape variables, characterising the longitudinal and transverse momentum componenents (thrust and jet broadening), the jet invariant mass or hadron-hadron correlations ($ C$ parameter). These infrared safe observables are in principle calculable as subsequent emissions of quarks and gluons. They represent an interesting interplay between the perturbatively calculable hard sub-process and the non-perturbative hadronisation effects. Perturbative calculations of event shape distributions have become available in next to leading order (NLO) in the strong coupling $ \alpha _s$ including resummed contributions to account for higher orders. Hadronisation corrections are traditionally applied by using phenomenological Monte Carlo models. In the present study an alternative approach, the concept of power corrections, has been choosen. This is an ambitious program to extend perturbative methods into the non-perturbative regime, i.e. one tries to describe hadronic final states analytically in terms of Feynman diagrams. Confinement is parametrised by introducing one additional constant, an average infrared coupling $ \alpha_0$, replacing the usual strong coupling below some low scale. Power corrections, which decrease with energy as $ 1/Q$, provide a much cleaner connection between parton and hadron levels compared to models.

Indeed, the observed event shape distributions are very well described over a large range of values and energy scales; an example of the jet broadening is shown in figure 1.

Figure 1: Normalised event shape distributions for the jet broadening $ B$. H1 data are compared with fits based on NLO QCD including resummation and supplemented by power corrections.
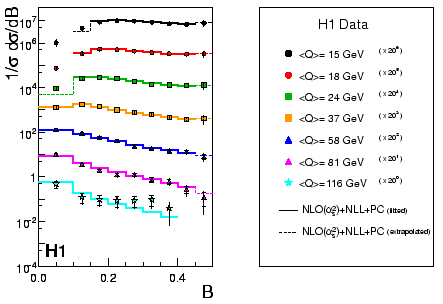\begin{figure}\centering \epsfig{file=d05-225f1col.eps, bbllx=0pt,bblly=0pt,bburx=600pt,bbury=410pt,clip=,% angle=0,width=.8\textwidth} \end{figure}

A QCD analysis based on resummed NLO calculations supplemented by power corrections yields consistent results for the strong coupling constant $ \alpha _s$ and a universal non-perturbative parameter $ \alpha_0$ for all event shape variables. A combined two-parameter fit yields

$\displaystyle \alpha_s (m_Z)$ $\displaystyle =$ $\displaystyle 0.1198 \pm 0.0013\ ({\rm exp})\ ^{+0.0056} _{-0.0043}\ ({\rm theo}) \ ,$  
$\displaystyle \alpha_0$ $\displaystyle =$ $\displaystyle 0.476 \pm 0.008 \ ({\rm exp})\ ^{+0.018} _{-0.059}\ ({\rm theo}) \ .$  

This result on the strong coupling shows a level of experimental precision competitive with determinations from other collider measurements and it is compatible with the current world average. The errors are dominated by the theory uncertainty, related to missing higher order terms in the perturbative calculation.

Another important outcome is the running of the strong coupling $ \alpha_S(Q)$ over a wide range of $ Q = 15 - 116\,{\rm GeV}$ in a single exeperiment, as demonstrated in figure 2.

Figure 2: The strong coupling $ \alpha _s$ as a function of the scale $ Q$ from an average of fits to the differential event shape distributions. The individual results are compared with a common fit, the shaded areas represent experimental and theoretical uncertainties.
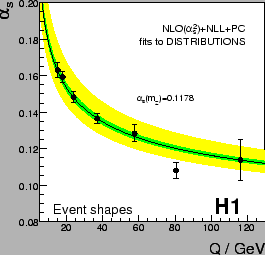\begin{figure}\centering \epsfig{file=d05-225f6.eps, angle=0,width=.8\textwidth} \end{figure}

These results are a beautiful support of the concept of power corrections. Note, that the universal behaviour of power corrections has also been shown for the mean values of event shape variables in this and a dedicated previous analysis, as well as in $ e^+e^-$ experiments.