 |
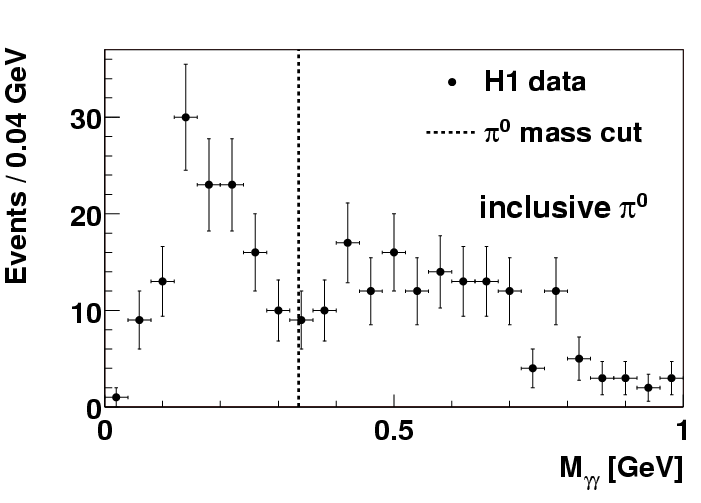
| The figure shows the invariant mass distribution of two-photon candidates for inclusive events before the full event selection, proving that we are able to see neutrel pions. |
Search for Odderon-Induced Contributions to Exclusive pi0 Photoproduction at HERA |
This is evidently in contradiction to experimental observation. In order to reconcile experiment and Regge phenomenology, a new trajectory, the "Pomeranchuk trajectory" or simply "Pomeron", was introduced with an intercept slightly above one so that cross section can slowly rise. The Pomeron carries the quantum numbers of the vacuum, especially C = P = +1. Note that the Pomeron is not a particle, neither real nor virtual! However, one might expect to find real particles, namely glueballs, lying on the Pomeranchuk trajectory.
The Pomeron was named after the Russian theoretician I. Ya. Pomeranchuk, famous for his "Pomeranchuk Theorem". This conjecture stated that at asymptotically large energies the difference between hadron - hadron and hadron - antihadron total cross section vanishes, and here the story of the Odderon (introduced by L. Lukaszuk and B. Nicolescu 1972) begins!
Whilst Regge phenomenology is the best means that we have of describing soft hadronic interactions, Quantum Chromodynamics (QCD) gives us a microscopic theory of the strong interaction where the structure of the hadrons is resolved. QCD does indeed allow for the exchange of yet another trajectory carrying C = P = -1, called the "Odderon". If it contributes to e.g. high energy proton - proton and proton - antiproton interactions, then, due to its different coupling to protons and antiprotons, a finite difference between proton - proton and proton - antiproton total cross sections should survive. In the rather limited data available this difference has not yet been observed: The Odderon either has only a tiny influence, or even does not exist.
After talking so much about hadron - hadron scattering, one might wonder how and why HERA comes into the game. But it is electron - proton scattering (or, better it's by-product, photon - proton scattering, known as photoproduction) which opens a window where one might look for the Odderon's traces: It was a group of theorists led by H. G. Dosch and O. Nachtmann in Heidelberg who first thought about this possibility. In photoproroduction, pomeron (C = P = +1) exchange leads to `exclusive' vector meson production, processes such as gamma p --> rho0 p, where the produced vector meson (rho0 in this case) has the same quantum numbers as the photon. If the exchanged Pomeron is replaced by the Odderon (C = P = +1), then, in order to conserve all quantum numbers, the vector meson has to be replaced with e.g. a pseudoscalar. The simplest case is a pi0. Other pseudoscalars would also do the job, and even some tensor mesons, but here we will restrict ourselves to the neutral pion. Our theorists predict a sizeable coupling of the Odderon if the proton in the reaction is excited and converted into an N* (i.e. a proton excitation with isospin 1/2). The reaction to look for is then gamma p --> pi0 N*, and so we have now all ingredients to fish for the Odderon:
We have to find the scattered electron in the small angle electron detector ("electron tagger") of H1 which ensures that our reaction is of the photoproduction type. We have to identify the pi0, i.e. we have to reconstruct its rest mass from the decay photons (more than 99 % of all pi0's decay into two photons). For this purpose we make use of the two H1 backward (that means covering the electron downstream beam direction) calorimeters, the big SpaCal and the small VLQ ("Very Low Q2") calorimeter which covers a small polar angular region around the electron beam direction. Finally, we have to prove that there was an excited proton: If we measure a leading neutron we know that it was from an N* decay; other possibilities such as Delta isobars need to be produced via the exchange of mesons with non-zero isospin, which are expected (Regge theory!) to be negligible at HERA energies. The high energy neutron is measured in a device called the "Forward Neutron Calorimeter" which is located about 100 m upstream in the proton beam direction. We perform our analysis on the basis of an integrated luminosity of about 30 pb-1 collected in the years 1999 and 2000. A simulation based on the theoretical calculation predicts a number of roughly 100 events produced by Odderon exchange.
What do we see? First, we demonstrate (Fig. 1) that we are able to reconstruct pi0's in our backward calorimeters: The figure shows a clear peak in the two-photon invariant mass close to the nominal mass. At least one of the two photons must be measured in the VLQ because this is a condition for the trigger. To produce this distribution, only minimal cuts have been used so that this plot represents an "inclusive" rather than an "exclusive" measurement; i.e. other particles are allowed in addition to the pi0.
Now, when tightening the cuts in order to guarantee the "exclusiveness" of the reaction (Fig. 2), we see that only a handful of pion candidates is left, in strong contrast to what is expected from theoreticians' prediction which is also shown in the figure. Such a rather negative finding is generally presented in terms of upper limits, and when we convert the number of observed events (assuming no background to be conservative) into a cross section we arrive at an upper limit for Odderon induced single pi0 photoproduction of 49 pb (at the 95 % confidence level), which has to be compared to a predicted value of over 200 pb (integrated over the in H1 accessible phase space).
There are several possibilities to interpret this result:
The Odderon trajectory might not have the same intercept as the Pomeron,
which is implicitly assumed here, so that photon - Odderon fusion simply
"dies out" at HERA energies. Or the photon - Odderon - pion coupling might
be much weaker than anticipated in the theoretical model. The solution
that no Odderon exists at all would be hard to accommodate within QCD -
so the chase must go on! The next step at HERA might be to search for
exclusive tensor meson
(f2, a2) photoproduction.
 |
| The figure shows the invariant mass distribution of two-photon candidates for inclusive events before the full event selection, proving that we are able to see neutrel pions. |
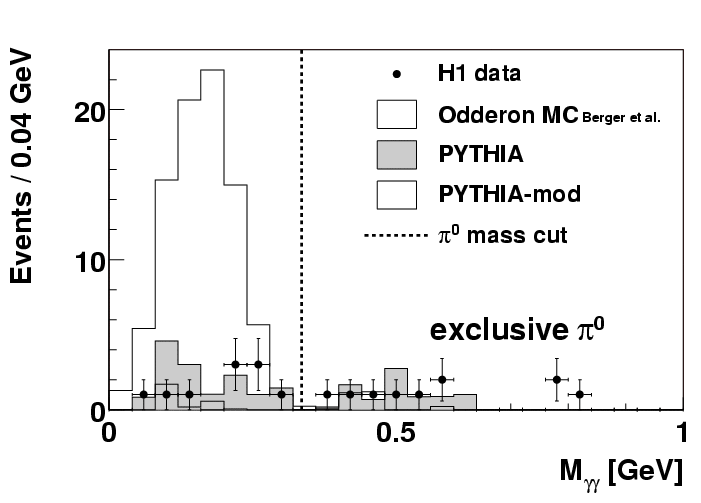 |
| The figure shows the invariant mass distribution of two-photon candidates for exclusive events for the data and the expected background and Odderon signal. |