Deep-inelastic Inclusive ep Scattering at Low x and a Determination of alpha_s

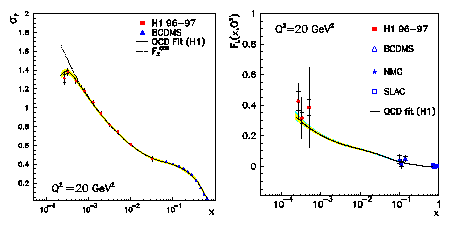Figure 1: Measurement of the "reduced" deep-inelastic scattering cross section (left), here given for example at Q²=20 GeV² by the H1 experiment at low x (solid points) and by the fixed target µp experiment BCDMS at larger x (triangles). The curves represent the QCD calculation of the cross section (solid) and of the structure function F₂ (dashed) which in most of the x range is identical to the cross section. At lowest x the cross section is lower than F₂ which is attributed to the longitudinal structure function F_L. From the difference of the data points and the calculated, extrapolated F₂ a measurement of F_L is derived (right).

By using large scale detectors, the HERA collaborations measure the inclusive deep-inelastic scattering cross section amounting to a measurement of the rate at which the beam electrons recoil from the quarks inside the protons. This rate depends on the photon virtuality Q² and on the fraction of proton momentum x carried by the struck quark. Due to the colliding beam kinematics, HERA has extended the range explored in deep-inelastic scattering by orders of magnitude into the new region of extremely low x. This paper presents a first precise measurement of this scattering cross section and confronts it with the expectation from Quantum Chromodynamics (QCD), a modern field theory, which describes strong interactions as the exchange of coloured gluons between quarks inside the proton.

The unknown proton structure is measured by two structure functions, F₂ and F_L, which correspond to different polarisation states of the exchanged virtual photon. While the structure function F₂ in a large part of the measured kinematic region is identical to the deep-inelastic scattering cross section itself, the determination of F_L is experimentally much more challenging. Its effect is seen for example in figure 1 (left), where the deviation of the measured cross section points from the extrapolation of F₂ (dashed line) signals the onset of the contribution by the longitudinal structure function F_L. The derived data points on F_L are shown in figure 1 (right) demonstrating again the large extension of the kinematic range.

The photons which mediate the electromagnetic interaction do not couple directly to electrically neutral gluons but to charged quarks. However, the presence of gluons inside the proton can be felt by the struck quark. At large quark momenta x, quarks can have lost sizable momentum by radiating gluons prior to the interaction with the virtual photon. Gluons can produce pairs of sea quarks which enhances the amount of quarks available for interaction with the photon at low momenta x. These processes can be resolved if the resolution of the photon probe, determined by its virtuality Q² is sufficiently large. The amount of quark scattering partners is thus expected to increase with Q² , i.e. at low x the structure function F₂(x,Q²) should rise with Q², and this rise is determined by the gluon momentum distribution. As can be seen in figure 2, these so-called scaling violations are indeed observed and they are well described by the theoretical calculation using QCD.

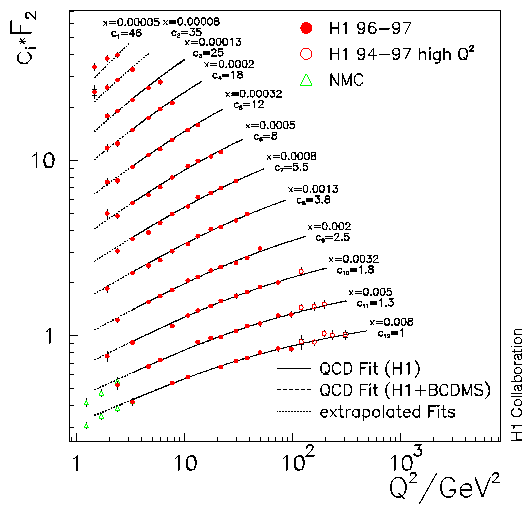Figure 2: Measurements of the proton structure function F₂(x,Q²) by the H1 and the NMC experiments. Solid curves indicate the QCD expectations. Dotted curves show fit extrapolations at fixed x into the region below Q²=3.5 GeV²
Through the production of sea quarks, the distribution of gluons becomes thus measurable. Figure 3 shows the gluon distribution for three values of Q². As can be seen, the gluon distribution rises dramatically towards low values of x reflecting the strong Q² dependence of F₂. At some point, this rise towards low x must come to an end since only a finite number of gluons can be accommodated in a proton. This, however, has not been observed yet, and it is to be seen in future accelerator experiments where a damping of this rise may set in.

In any field theory the coupling constant determines the strength of the interaction. Over three decades it has been attempted to accurately measure the strong interaction coupling constant alpha_s. In the last part of this paper a phenomenological analysis is presented leading to one of the most precise determinations of alpha_s obtained so far. This accuracy is not surprising given the large kinematic range of the new HERA data combined with the BCDMS data, the high precision of these measurements and the theoretical advantages of inclusive deep-inelastic scattering for testing Quantum Chromodynamics.

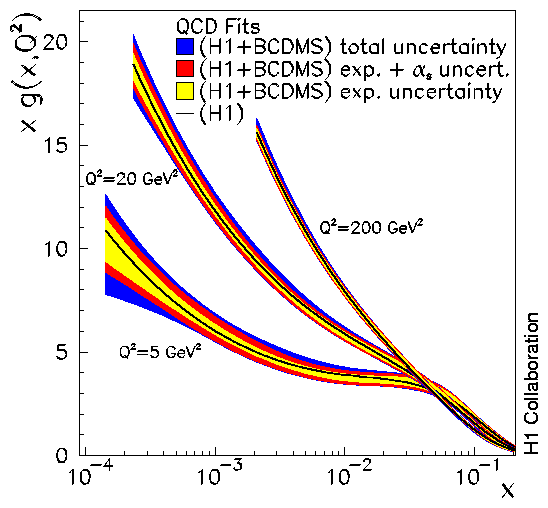Figure 3: Gluon distribution resulting from the QCD fit to H1 ep and BCDMS µp cross section data. The innermost error bands represent the experimental error for fixed alpha_s=0.1150. The middle error bands include in addition the contribution due to the simultaneous fit of alpha_s. The outer error bands also include the uncertainties related to the QCD model and data range. The solid lines inside the error band represent the gluon distribution obtained in the fit to the H1 data alone.

Last Update 11.12.2000